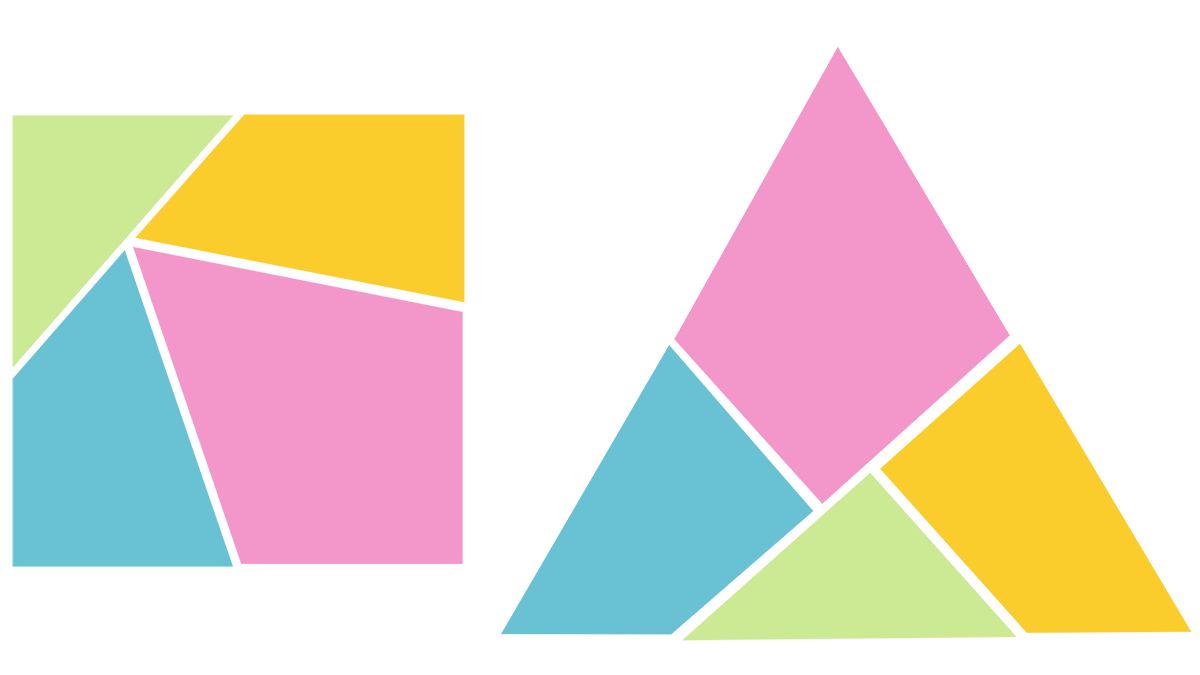За кажущейся статичной формой скрываются связи, преобразования и, прежде всего, элегантность математики.

В 1902 году английский математик Генри Эрнест Дудени (1857–1930) предложил в своей колонке головоломок в газете Weekly Dispatch — известной как Sunday Dispatch с 1928 по 1961 год, когда она слилась с Sunday Express — задачу, которая, казалось бы, проста, но скрывала за собой увлекательную сложность: как разделить равносторонний треугольник на минимальное количество частей так, чтобы, переставляя их (только путем перемещения и вращения, без наложения), можно было сформировать идеальный квадрат?

Один из читателей, Чарльз Уильям МакЭлрой, предложил остроумное решение с использованием всего четырех частей, соединенных вершинами и шарнирами, создав своего рода механический пазл, который позволял простым поворотом превратить треугольник в квадрат. На протяжении последних 122 лет никто не смог достичь того же результата с меньшим количеством частей, хотя также не было никаких указаний на возможность такого решения.

Если и были сомнения, они исчезли в декабре 2024 года, когда математики Тонан Камата и Рюхей Уэхара из Японского института передовых наук и технологий, а также Эрик Д. Демейн из Массачусетского технологического института, доказали, что невозможно решить эту задачу менее чем с четырьмя частями. Таким образом, решение, предложенное МакЭлроем и Дудени более века назад, является «оптимальным» — или, другими словами, более эффективное решение невозможно.

Чтобы разгадать эту геометрическую загадку, Камата и его коллеги-математики свели ее к проблеме теории графов. Вместо попыток бесконечных комбинаций геометрических разрезов, они ограничили задачу анализом возможных разрезов как графов. Напомним, что граф — это математическая структура, состоящая из вершин (также называемых узлами или точками), соединенных ребрами (также известными как дуги, связи или линии). Теория графов — это раздел математики, изучающий графы. Вернемся к геометрической загадке: каждый разрез исходного равностороннего треугольника представлен как ребро, а каждая точка пересечения — как вершина. Благодаря этому они смогли классифицировать все возможные вариации в управляемые категории, сведя бесконечную проблему к конечному набору случаев. Результат вам уже известен.

Помимо своей теоретической ценности, это открытие имеет значение для таких разнообразных областей, как дизайн, архитектура и даже педагогика математики. Например, лондонское архитектурное бюро DHaus воплотило головоломку Дудени — также известную как «разрез Дудени» или «проблема торговца», последнее название связано с тем, как сам Дудени представил ее в виде задачи №26 в книге The Canterbury Puzzles (1907), где торговец бросает вызов своим собеседникам, предлагая разрезать кусок ткани в форме равностороннего треугольника, чтобы сформировать идеальный квадрат. Бюро DHaus, как мы уже упомянули, перенесло эту геометрическую игру в дизайн стола и дома с подвижными частями.

Как видите, задачи, кажущиеся простыми, могут скрывать неожиданные глубины. В любом случае, в следующий раз, когда вы увидите треугольник или квадрат, возможно, вы вспомните, что за их кажущейся статичностью скрываются неожиданные связи, удивительные преобразования и, прежде всего, вечная элегантность математики.

Источники: Arxiv.org, Scientific American, Wolfram MathWorld, Gutenberg.org, Wikipedia.
Изображения: DHaus 1, DHaus 2, Wikipedia.